INTRODUCTION:

Two dimensional arrays allow the programmer to solve problems involving rows and columns. Many data processing problems involve rows and columns, such as an airplane reservation system or the mathematical modeling of bacteria growth. A classic problem involving two-dimensional arrays is the bacteria program presented in the lab exercise, Life. After surveying the syntax and unique aspects of these larger data structures, such information will be applied to more challenging lab exercises.

The key topics for this lesson are:

A. Two-Dimensional Arrays
B. Passing Two-Dimensional Arrays to Methods
C. Two-Dimensional Array Algorithms

VOCABULARY:

MATRIX
COLUMN

ROW

DISCUSSION:

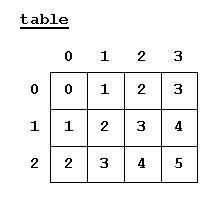
A. Two-Dimensional Arrays

1.Often the data a program uses comes from a two dimensional situation. For example, maps are two dimensional (or more), the layout of a printed page is two dimensional, a computer-generated image (such as on your computer's screen) is two dimensional, and so on.

For these situations, a Java programmer can use a two-dimensional array. This allows for the creation of table-like data structures with a row and column format. The first subscript will define a row of a table with the second subscript defining a column of a table. Here is an example program including a diagram of the array.

Program 19-1

class ArrayExample
{
  public static void main (String[] args)
  {
    int[][] table = new int[3][4];
    int  row, col;

    for (row = 0; row < 3; row++)
      for (col = 0; col < 4; col++)
        table[row][col] = row + col;
  }	
}

2. Two-dimensional arrays are objects. A variable such as table is a reference to a 2D array object. The declaration

int[][] table;

says that table can hold a reference to a 2D array of int. Without any further initialization, it will start out holding null.

3. The declaration

int[][]table = new int[3][4];

says that table can hold a reference to a 2D array of int, creates an array object of 3 rows and 4 columns, and puts the reference in table. All the elements of the array are initialized to zero.

4. The declaration

int[][] table = { {0,0,0,0},
                  {0,0,0,0},
                  {0,0,0,0} };

does exactly the same thing as the previous declaration (and would not ordinarily be used.)

5. The declaration

int[][]table = { {0,1,2,3},
                 {1,2,3,4},
                 {2,3,4,5} };

creates an array of the same dimensions (same number of rows and columns) as the previous array and initializes the elements to specific values.

6. If no initializer is provided for an array, then when the array is created it is automatically filled with the appropriate value: zero for numbers, false for boolean, and null for objects.

7. Just as with one-dimensional arrays, the row and column numbering of a 2-D array begin at subscript location zero (0). The 3 rows of the table are referenced from rows 0...2. Likewise, the 4 columns of the table are referenced from columns 0...3.

8. The two-dimensional table is filled with the sums of row and col. To access each location of the matrix, specify the row coordinate first, then the column:

table[row][col]

Each subscript must have its own square brackets.

9. The length of a 2D array is the number of rows it has. The row index will run from 0 to length-1. The number of rows in table are given by the value table.length.

Each row of a 2D array has its own length. To get the number of columns in table, you have to ask how many ints there are in a row; this number would be given by table[0].length, or equivalently by table[1].length or table[2].length. (There is actually no rule that says that all the rows of an array must have the same length, and some advanced applications of arrays use varying-sized rows. But if you use the new operator to create an array in the manner described above, you'll always get an array with equal-sized rows.)

10. Program 19-1 assumes its array argument has 3 rows and 4 columns. That is fine for this particular program, but a nicer definition would work for any array of any two dimensions.

Program 19-2

class ArrayExample2
{
  public static void main (String[] args)
  {
    int[][] table = new int[3][4];
    int  row, col;

    for (row = 0; row < table.length; row++)
      for (col = 0; col < table[row].length; col++)
        table[row][col] = row + col;
  }
}

In Program 19-2, the limits of the for loops have been redefined using table.length and table[row].length so that they work with any two-dimensional array of ints with any number of rows and columns .

B. Passing Two-Dimensional Arrays to Methods

1.1. The following program will illustrate parameter passing of an apmatrix. The purpose of this program is to read a text file containing integer data, store it in a 2-D array, and print it out. The contents of the text file "data.txt" is shown first:

"data.txt"

17   3   2  13
 5  10  11   8
 9   6   7  12
 4  15  14   1

Program 19-3

// A program to illustrate 2D array parameter passing
class Test2D
{
  static void printTable (int[][] pTable)
  {
    for (int row = 0; row < pTable.length; row++)
    {
      for (int col = 0; col < pTable[row].length; col++)
        System.out.print(Format.right(pTable[row][col], 4));
      System.out.println();
    }
  }
  
  static void loadTable (int[][] lTable)
  {
    TextReader inFile = new TextReader("data.txt");
    
    for (int row = 0; row < lTable.length; row++)
      for (int col = 0; col < lTable[row].length; col++)
        lTable[row][col] = inFile.readInt();
  }
  
  public static void main (String[] args)
  {
    final int MAX = 4;
    
    TextReader keyboard = new TextReader();
    
    int[][] grid = new int[MAX][MAX];
    
    loadTable(grid);
    printTable(grid);
  }
}

2. The loadTable and printTable methods use a reference parameter, (int[][] lTable and int[][] pTable respectively). The local identifiers lTable and pTable serve as aliases for the actual parameter grid passed to the methods.

3. When a program is running and it tries to access an element of an array, the Java virtual machine checks that the array element actually exists. This is called bounds checking. If your program tries to access an array element that does not exist, the Java virtual machine will generate an ArrayIndexOutOfBoundsException exception. Ordinarily, this will halt your program.

C. Two-Dimensional Array Algorithms

1. The most common 2-D array algorithms will involve processing the entire grid, usually row-by-row or column-by-column.

2. Problem-solving on a matrix could involve processing:

a. one row
b. one column
c. one cell
d. adjacent cells in various different directions

3. In the next lesson we will look at a 2-D recursive solution to a rather difficult problem.

SUMMARY/ REVIEW:

Two-dimensional arrays will be applied to two interesting problems. The simulation of life in a petri dish of bacteria will require a two-dimensional array representation. The second and third lab exercises are different versions of the "Knight's Tour" problem, an interesting and demanding chess movement problem.